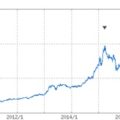
「複利」と「単利」。投資家であれば誰でも意識せずとも体が理解している言葉(感覚)ですが、以外にも投資経験のない人にとっては理解してない人が多い様です。
今回は言葉の意味、複利的思考、複利に関するいくつかの話しをしてみたいと思います(ノ)・ω・(ヾ)
アインシュタインと「複利」

これはあまりにも有名な話しですが、僕が超がつくほど尊敬して止まない人類史上最高峰の頭脳を持ったアルベルト・アインシュタインが「人類史上最大の発見は?」と記者に聞かれ「複利の力だ」と答えたそうです。
では、人類史上最高の天才に最大の発明と言わした「複利の力」とは一体何なのか?
少しずつ話しを進めたいと思います(`・ω・´)
単利とは? 複利とは?
現代社会の経済システムでは「複利」は当たり前すぎて意識すらしてないかもしれませんが、「複利」と「単利」(対義語)の違いをしっかり理解しておく事は投資をやらない人でも、お金だけではなく人生を色んな意味で豊かにすると思います。
人間関係においても必ずや役に立つ事と僕は思っています。
単利とは?
簡単に言うと、元本にだけ利子をつける計算方法の事を「単利」と言います。
あまり、金融や投資に興味がない方はこれでもパッとしないかもしれないので、少し具体的な数字を出してみたいと思います。
100万円の元本(自己資金)を、1年で利回り20%の単利金融商品を購入するとします。
この場合、1年間で100万円×0.2(20%)= +20万円
2年目も同じ計算方法なので+20万円で合計すると140万円になりますね。
では、この調子で10年間続けると合計いくらになるでしょうか?
100万円×2(20%×10年間分)=200万円
元本の100万円と合わせると300万円になりましたね☝
それと以外かと思われるかもしれないですが、日本で発売している投資信託は5000以上はあるのかなぁ🤔
僕の知ってる限り99%は、この単利で運用されているので、これから購入を考えている方はこの点にも注意が必要ですね☝
複利とは?
では複利とは何なのか?
これもまた簡単な言葉で言うと、元本と前年の利子をプラスしたものに対して利子がついていくという計算方法の事を「複利」と言います。
言い換えると、前年に出た利益を全て再投資していくという事です。
では「単利」と同じ条件で数字を当てはめていきましょう。
最初の一年目
100万円×0.2(20%)=20万円
これは単利と変わらない数字ですね
では2年目を見ていきましょう。「複利」とは前年の利益も合わせて計算する事です
120万円×0.2(20%)=24万円
合計で144万円になりましたね。
あれっ!
「単利」の計算式と比べてもらうと分かると思いますが、既に4万円の違いがでてきています。
ではこの調子で10年後の「複利」はどうなっていくのか・・・
何と10年後「複利」の20%を続けていくと、ざっくりと619万になります。
単利運用では300万円
複利運用では619万円
なかなかの違いです。更にいってみましょう👉
30年間の運用ではどうなるか?
単利運用では700万
複利運用では2億3700万(端数切り)
いや、実際に「単利」と「複利」ではこれだけの数字上の違いがでてきてしまうのです。
机上の空論になってしまいますが、実際に実践した大物投資家もまだ健在です。
ウォーレンバフェット(超大物長期投資家)

バフェットも必ず別の機会に取り上げたいので詳しい事は書きません。(尊敬して止まない投資家の一人です)
バフェットは、僕が複利計算で使った数字をそのまま実践した人です。
確かに複利計算で100万円が20%の利回りで30年間で2億を超える計算になるので、平均22%の運用を続ければバフェットの年齢からいっても6兆円は頷けます🐱☝
実際に利回り20%の金融商品はなかなか表に出て来づらいですが、不動産物件では以外にゴロゴロしてるものです。
もちろん僕も20%利回りの物件はいくつも所有してますが、毎年の利益を全てオールインしてるかと言えば、そうではないので「単利?」、ん〜「複利」との中間くらいのスタンスで投資をしています。
まぁ、そこそこ資産は膨らんでいっているので「複利の力」を利用しているという事でしょう。
複利、「72の法則」を知ろう
前章で利回り20%の金融商品はなかなか出ないと言いましたが、その通り「なかなかそんなものはありません。」
都市銀行の利回り0.01%なんてものを見れば、20%の利回りが、どれほどスゴイ数字か分かると思いますが(僕に言わせれば銀行のゼロ金利が異常すぎる)、単純なはなし利回りが上がれば上がるほどリスクが上昇するという基本的な考え方に間違いはないと思うので、それぞれに合った力量で投資対象を選択していかなければいけません🧐
おっとまた話がそれていく💦
実は利回り計算で非常にわかりやすい目安となる数字があります。
72の法則「72÷金利=年数」
これは元金(投資資金)が何年で倍になるかを知るのに便利な計算式です。
もし、利回り7.2%の金融商品を「複利」で運用した場合、
72÷7.2=10
10年間で元金が倍になるという事です。
1000万を7.2%で運用すれば10年後には2000万になっているという事ですね😋
株式投資の過去の平均利回りは7〜10%程度なので長期で運用した場合、倍にするくらいであればとても現実的な数字になりますね。
更にこの利回りを続けていけば10年ごとに倍になるので、20年で4倍、40年で16倍と加速度的に資産が膨らんでいきます。
先程の1000万であれば40年後には1億6000万になるというのも無理のない現実的な数字だという事が分かると思います。
短期的な目線しかない人は100万の利益程度で喜んで利確するところを、「複利の力」を知っている人々は、たくさん蒔いた種が本当の大木になるまで決して刈ろうとはしないのです。
「お金は寂しがりやだ、たくさんある所に集まってしまう」という言葉も、あながち嘘ではなく、この「複利の力」を表現した言葉だと僕は思っています。
ちなみにあまり話したくはなかったのですが、2018年現在一般的な都市銀行の金利は0.01%もあるかないかだと思います。さて、倍にするには何年かかるのか?先程の計算式に当てはめてみると、
72÷0.01(金利)=7200(年)
7200年・・・😱💦
何ともオメデタイ数字がでてきてしまいました・・😨
お金に対する考え方は人それぞれ、僕の様な計算をする人間の事を毛嫌いする人も沢山いると思いますが、それでもなお全額普通預金(定期も同じ)に置いておくなんて事は、「複利の力」を知っている僕からすればあり得ない事となります。
ちなみに僕は、必要以上にお金を増やすという様な事をしないと常に心がけています。
それは、お金で「幸せ」は絶対に買えるものではない。
お金はなさすぎても辛いが、ありすぎるのもまた苦労をする、少しないぐらいが1番楽しいんだという事を経験上知ってるからかもしれません。
複利的思考を応用する
「複利的思考」なんて言葉が存在するかも良く分かりませんが、この思考を身につけるだけで生活のいたる所で応用が効くんじゃないかと僕は思っています。
複利的思考 CASE1
ビジネスの場でも複利的思考は役に立ってきます。
例えば、複利的思考を持つ僕と、そうではないA君の単純比較をしてみたいと思います。
「複利的思考」を持つ僕と、ガムシャラ熱血のA君は新入社員で営業成績を上げたくて日々頑張っています。A君はひたすら電話勧誘と足を使って営業をかけていきます。真夏の炎天下も真冬の凍える日も休みの日もガムシャラに頑張るA君。
僕は定時で帰宅し休みはしっかり取り、マイペースながらA君ほどではないにしろ頑張ります。
心強い言葉です。家族の応援は実に励みになります。
さて、数ヶ月が経過した辺りから成績に傾向が表れ始めました。
熱血A君は、そこそこの営業成績です。ノルマを切る事はないにしろ、毎月同じくらいの営業成績をキープしている様です。
一方僕の営業成績は月日が経つにつれどんどん良くなっていきます。3年程経過した時には、僕とA君では10倍以上の成績の差が毎月でるようになってしまいました。
さてどういう事でしょうか?
上の章の「単利」と「複利」の効果を読んだ方ならすぐに分かると思います。
「複利的思考」魔法の言葉
僕は契約してくれた取り引き相手にはもちろんの事、契約までいたらなった相手にも話を聞いてくれた方には、ある魔法の言葉を口にしていました。
実は魔法の言葉なんていう大層なものではありません。
「もし我が社の商品に興味がありそうな方がいらしたら、是非紹介してくれたら助かります」
その一言だけです。
そして丁寧に頭を下げる🙇オネガイシマス
10人中9人は社交辞令的に頷きすぐ忘れてしまうでしょう。ただその内の1人でも興味のある人を紹介してくれ契約まで至る。あとは分母の増加、時間の経過と共に加速度的に契約が増えていく。
もちろん営業の契約とは、そんなに単純なものではありません。様々なスキル、取り引き相手に対する「気づかい」やマージン🤢?! コミニケーション能力などの結果による所も多いですが、ここで言いたい事は、A君の様に1人でガムシャラに頑張っても1人の力では毎年、同じ成果しか出せないという事です。
この記事で言うところの「単利的思考」です。
一方「複利的思考」を持つ僕は、たった一言の魔法の言葉と時間を味方につけ加速度的に成果を上げていく。
この考え方こそ「複利的思考」。
この思考はビジネスのシーンに留まらず、目指す自分、目的に応じてにさまざまな応用ができると思います。
さて、ここでの「複利的思考」がどんなものかと言うと・・
やはり信用のおける友達に「誰かいい人いたら紹介して」になってしまうんでしょうかねぇ🤔
・・・、
・・・・そう言えばドラちゃんはどこで出てくるの?
あっっっ‼️
タイトルのドラえもん出すの忘れてた😱💦
また一気に書いてたから着地点間違えた😱💦
あ〜ん、長くなりすぎたし眠いから😪💤、ドラえもんの複利話はまたいつか・・・・

・・・・💧
そんな顔しないでぇ~~😭
嗚呼、可愛らしいドラちゃん😢💕
いや💦、たいした話じゃないけど次回記事にしたいと思います🙇 ガラガラ~